Le transistor : Valeurs booléennes
Les portes sont les principaux composants des circuits qui manipulent des données binaires.
Les portes logiques sont des circuits qui possèdent des sorties et des entrées sur lesquelles on va placer ou récupérer des bits. Les entrées ne sont rien d'autre que des morceaux de « fil » conducteur sur lesquels on envoie un bit (une tension). À partir de là, le circuit électronique va réagir et déduire le bit à placer sur chaque sortie. Tous les composants d'un ordinateur sont fabriqués avec ce genre de circuits.
Le transistor est le composant principal des portes logiques le circuit de base d’un ordinateur aujourd'hui. Il est utilisé dans deux états particuliers de fonctionnement qui dépendent de la tension appliquée à ses bornes :
son régime saturé (le transistor est passant : il se comporte comme un interrupteur fermé),
son régime bloqué (le transistor est bloquant : il se comporte comme un interrupteur ouvert).
À ces deux états, on fait correspondre les valeurs booléennes (logiques) : \(0\) et \(1\).
Opérateurs booléens
1. Les opérateurs de base
Une variable booléenne ou variable logique est une variable dont la valeur est soit \(0\) soit \(1\).
En logique, \(0\) est aussi représenté par FAUX (False) et \(1\) par Vrai (True).
un opérateur booléen (ou porte booléenne) est un circuit intégré spécialisé destiné à réaliser une opération booléenne. Pour un tel circuit, on fait correspondre aux signaux électriques existants en entrée et en sortie, un état logique valant \(0\) ou 1. En électronique positive, l’état 0, correspondant à la présence d’une tension inférieure ou égale à un certain seuil (le tiers environ de la tension d’alimentation) tandis que l’état \(1\), correspondant à la présence d’une tension supérieure ou égale au deux tiers de la tension d’alimentation.
2. L'opérateur \(non\) (\(not\) en anglais)
Cet opérateur permet de représenter la négation d’une proposition : si une proposition est vraie, alors sa négation est fausse, et réciproquement.
Notation :
\(non\) \(a\) \(=\) \(not\) \(a\) \(=\) \(\overline{a}\) \(=\) \(¬a\)
Sa table de vérité (tableau qui récapitule les valeurs de sortie en fonction des valeurs d’entrée) est
| \(a\) | \(not\) \(a\) |
|---|---|
| \(0\) | \(1\) |
| \(1\) | \(0\) |
Représentation symbolique de l'opérateur \(not\)

Remarque :
L’opérateur \(non\) est également appelé un inverseur.
3. L’opérateur \(ou\) (\(or\)) : la disjonction de propositions
La disjonction de deux propositions \(a\) et \(b\) est vraie si au moins une de ces deux propositions est vraie.
Autrement dit, la disjonction de deux propositions n'est fausse que lorsque ces deux propositions sont fausses.
Notation :
\(a\) \(ou\) \(b\) \(=\) \(a\) \(or\) \(b\) \(=\) \(𝑎\) ˅ \(b\) \(=\) \(a\) \(+\) \(b\)
Sa table de vérité est :
| \(a\) | \(b\) | \(a+b\) |
|---|---|---|
| \(0\) | \(0\) | \(0\) |
| \(0\) | \(1\) | \(1\) |
| \(1\) | \(0\) | \(1\) |
| \(1\) | \(1\) | \(1\) |
Représentation symbolique de l'opérateur \(or\)

4. L’opérateur \(et\) (\(and\)) : la conjonction de propositions
La conjonction de deux propositions \(a\) et \(b\) n’est vraie que si les deux propositions sont vraies. Elle est fausse dans les autres cas.
Notation :
\(a\) \(et\) \(b\) \(=\) \(a\) \(and\) \(b\) \(=\) \(𝑎\) ˄ \(b\) \(=\) \(a.b\)
Sa table de vérité est :
| \(a\) | \(b\) | \(a.b\) |
|---|---|---|
| \(0\) | \(0\) | \(0\) |
| \(0\) | \(1\) | \(0\) |
| \(1\) | \(0\) | \(0\) |
| \(1\) | \(1\) | \(1\) |
Représentation symbolique de l'opérateur \(and\)

Expressions booléennes
1. Définition :
Une expression booléenne est définie à l’aide de la combinaison des opérateurs de base (\(not\), \(and\) et \(or\)).
Les opérateurs de base sont également des expressions booléennes.
2. Exemples :
Si on note \(h\) la fonction \(or\), alors on peut l’écrire \(h(𝑎,𝑏)\) \(=\) \(𝑎\) \(ou\) \(𝑏\) \(=a+b\)
Faites-vous plaisir 1 !
-
Démontrer à l’aide des tables de vérité que les expressions suivantes sont équivalentes :
\(𝑓(𝑎,𝑏)\) \(=\) \(𝑛𝑜𝑡\)\((\)\(𝑎\) \(𝑎𝑛𝑑\) \(𝑏\)\()\)
\(g(𝑎,𝑏)\) \(=\) \(𝑛𝑜𝑡\) \(𝑎\) \(or\) \(𝑛𝑜𝑡\) \(𝑏\)
Même question pour les expressions :
\(𝑓(𝑎,𝑏)\) \(=\) \(𝑛𝑜𝑡\)\((\)\(𝑎\) \(or\) \(𝑏\)\()\)
\(g(𝑎,𝑏)\) \(=\) \(𝑛𝑜𝑡\) \(𝑎\) \(and\) \(𝑛𝑜𝑡\) \(𝑏\)
Faites-vous plaisir 2 !
Donner la table de vérité de l’expression \(f=\overline{a}.b+a.\overline{b}\)Remarque :
cette expression correspond à la porte \(xor\)
Notation : \(\overline{a}.b+a.\overline{b}=a\oplus b\)
Représentation symbolique de l'opérateur \(xor\)

À l'aide d'une phrase, dire dans quel cas l'opérateur \(xor\) retourne vrai.
Faites-vous plaisir 3 !
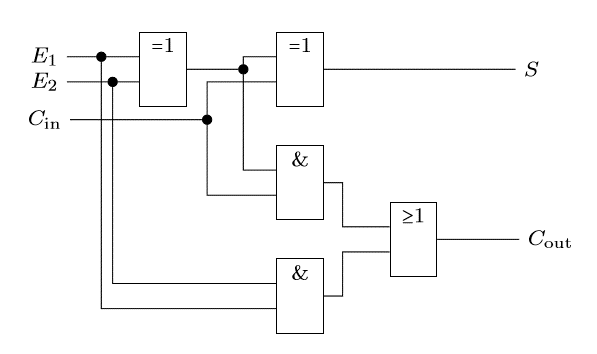
Donner la table de vérité du circuit logique suivant :
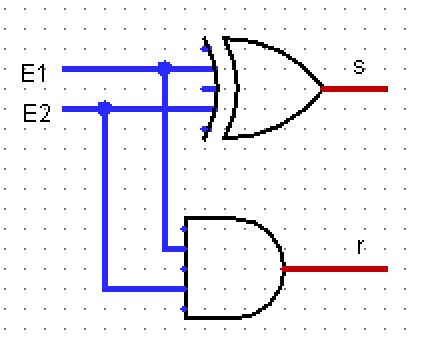
Faites-vous plaisir 4 !
Donner la table de vérité du circuit logique suivant :